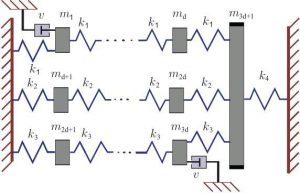
Within this part of the project we will consider dynamical systems described by PDEs or ODEs that model vibrations of mechanical devices or general engineering constructions. These systems are usually called vibrational systems. A simple example of a vibrational system is given in Figure 1. The aim is to further develop a corresponding mathematical theory, which will help us to pose and answer questions connected with the various control problems of practical interest that present state-of-the-art methods we cannot deal with. Special consideration will be given to the questions of optimal control of undesired vibrations, since it is a very important issue in many real-life applications.
As an important field of research, vibrational systems are a well-studied topic in engineering and mathematics and are an important topic in the field of control theory. In recent years vibrational systems theory experienced a new impetus and progress due to the results on optimal damping of homogeneous vibrational systems, the research in which some members of this project played an important role.
Our goal will be to extend the results for the homogenous systems obtained by the project members to the systems with external input, as well as to develop new directions of research, encompassing topics of control of distributed systems, control of linear parametrically-varying (LPV) systems, model reduction for LPV systems and finite horizon control. These topics are both highly important and with large number of applications.