The aim of the adaptive dual control is to automatically adjust the controller parameters in the case of both unknown and time-varying process parameters such that a desired degree of the performance index is met. Adaptive control systems are characterised by their ability to tune the controller parameters in real time exploiting the measurable information within the closed-loop system. Most of the adaptive control schemes are based on the separation of parameter estimation and controller design. This means that the identified parameters are used in the controller as if they were the real values of the unknown parameters, whereas the uncertainty of the estimation is not taken into consideration. This approach is known as the certainty-equivalence (CE) principle and is mainly used in adaptive control systems today. In 1960, A. Feldbaum indicated that adaptive control systems based on the CE approach are often far away from being optimal. Instead of the CE approach, he introduced the principle of adaptive dual control.
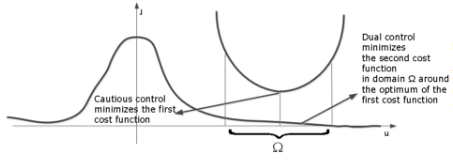
Due to numerical difficulties in finding simple recursive solutions of the Feldbaum’s stochastic optimal adaptive dual control problem, various suboptimal and modified adaptive dual control schemes had been proposed. One of the most efficient approaches among those is given by the bicriterial synthesis method for dual adaptive controllers. This bicriterial approach was first introduced by Filatov and Neuhausen. The main idea of the bicritical approach consists of introducing two cost functions that correspond to the two goals of dual control: (i) the system output should track cautiously the desired reference signal; (ii) the control signal should excite the plant sufficiently in order to accelerate the parameter estimation process (see Figure 2). These two cost functions represent control losses and an uncertainty index for the parameter estimates, respectively. Minimization of the first one results in cautious control action. Minimization of the uncertainty index provides the system with optimal persistent excitation. It should be noted that the minimization of the uncertainty index is realized in the domain around the optimal solution for the first criterion and the size of this domain determines the magnitude of the excitation. Therefore, the designed systems clearly achieve the two main goals of dual control. Moreover, the designed controllers are usually computationally simple to implement. Resulting dual controllers have one additional parameter that characterizes the magnitude of the persistent excitation and can easily be selected because of its clear physical interpretation.
In addition to the aforementioned challenges, the objectives of adaptive dual control in real-life applications typically need to be attained in degraded information environments. Consequently, the presence of sampled, noisy, partial, delayed and lossy information renders the adaptive dual control objectives (i) and (ii) yet more challenging. The phenomenon of realistic information environments has recently spurred a great deal of interest within the control system community.As stated in these references, realistic data exchange has detrimental effects on control system performance and on convergence properties. A similar robustness analysis in a different context is found in WP2, which speaks in favour of its importance. Consequently, we expect that some results obtained in WP3 will be applicable to WP2 and vice versa (e.g., Lp-stability from WP3 and dissipativity from WP2 are related stability notions).It is to be noted that the existing literature focuses either on adaptive dual control or degraded information environments, but not on both simultaneously. Thus, within this work package we plan to investigate how the interplay between adaptive dual control and degraded information impacts convergence and performance of the resulting dual controller.